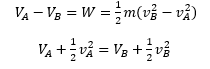EJERCICIOS INTERESANTES:EL MUELLE

Hoy en ejercicios interesantes...
EL MUELLE.

Un muelle de constante recuperadora k, masa despreciable y longitud en reposo lo
cuelga del techo.
Del otro extremo cuelga una masa m. Debido al peso, el muelle se estira.
Calcular la longitud que se ha estirado el muelle cuando la masa está en reposo.

El sistema se saca del reposo comunicándole una pequeña velocidad inicial en la dirección vertical.

Determinar la trayectoria de la partícula.

Bien, pasemos a resolverlo.
[1] Para calcular la longitud que se ha estirado el muelle desde la longitud en reposo hasta la longitud final aplicamos la ley de Hooke.
Debemos tener en cuenta que aquí actúan dos fuerzas, el peso de la masa que cuelga del muelle, que hace que el muelle se estire y la fuerza correspondiente a la compresión que se opone a ese estiramiento.

La longitud m se entiende como la longitud en reposo del muelle con la masa colgando y la longitud o sería la longitud del muelle en reposo sin masa.

Los vectores están claros, el peso en el eje j lo hemos considerado positivo y la fuerza de compresión del muelle en el eje j también pero como se opone al muelle le he colocado el signo contrario.

La longitud que se haya estirado será la resta de esas dos longitudes así que esta parte del problema ya está resuelta.

[2] Bien, aquí entramos en la parte interesante del problema y esa es la de calcular su trayectoria.

En general cuando quieres calcular la trayectoria de una partícula observas la fuerza a la que se ve sometida y a partir de ahí integrando la aceleración en la segunda ley de Newton obtienes la trayectoria.

Aquí lo que ocurre es que el muelle se ve sometido a tres fuerzas distintas, el peso, la compresión y la fuerza que le aplicamos nosotros con esa velocidad inicial.

Así que vamos a escribir la ecuación con las tres fuerzas:

Tenemos el peso y la fuerza que aplicamos nosotros en el lado positivo del eje y y la fuerza de compresión, la fuerza recuperadora que ejerce el muelle en el lado negativo del eje y.
Bien, hecho esto, empecemos a desarrollar la ecuación hasta sacar la trayectoria del muelle.

1-Aquí tenemos la ecuación a desarrollar.
2-Empezamos desarrollándola sustituyendo cada término, hay que recordar que la fuerza recuperadora se obtiene de la ley de Hooke.
3-En este paso únicamente hemos sustituido la longitud del muelle en equilibrio sin la masa, lo hemos sustituido de la ecuación que obtuvimos en el apartado [1] del problema.
4-En este paso hemos seguido desarrollando la ecuación.
5-Hemos obtenido finalmente dicha ecuación, pero debemos seguir desarrollándola, porque necesitamos acabar sacando las longitudes en función del tiempo, que es lo que nos otorga la trayectoria
Para ello, seguiremos unos pequeños pasos en el desarrollo de la ecuación.

Por un lado, a la longitud del muelle en función del tiempo menos la longitud del muelle en equilibrio con la masa lo vamos a sustituir por z para poder trabajar mejor.

Y la aceleración la sustituiremos por la longitud con dos puntos arriba(pura notación para referirse a una función derivada respecto al tiempo).

A su vez esa longitud con dos puntos la sustituiremos por z con dos puntos arriba(1), ya que según la ecuación que escribimos en el paso anterior si derivamos todas las opciones en la misma vemos que la derivada segunda de l es igual a la de z ya que la longitud del muelle con la masa en reposo es una constante y por tanto su derivada primera ya directamente es 0(2).

Por tanto obtenemos una ecuación diferencial ordinaria homogénea:

Si ya he subido alguna entrada de ecuaciones diferenciales en este blog o en mi blog de matemáticas y necesitas repasártelas, adelante.

Siguiendo con la ecuación observamos tras ver que es una homogénea de segundo grado que tiene raíces complejas conjugadas y por tanto sus solución final es:

Que coincide, efectivamente con la ecuación de la trayectoria de un oscilador armónico.

Aclarar que hemos deshecho el cambio en la variable z.

Pero seguimos teniendo un problema y es la constante A.

Por suerte tenemos un dato que todavía no hemos usado en el problema y ese es la velocidad inicial que se le aplica al muelle.

Así que usaremos ese dato para conseguir esta constante y terminar el problema.

Lo primero que hemos hecho ha sido derivar la ecuación de la trayectoria para obtener la ecuación de la velocidad respecto al tiempo, esa ecuación derivada y poniendo la condición inicial de tiempo=0 en el inicio la hemos igualado a la ecuación que nos daba el problema.

Una vez hecho esto vemos que las ecuaciones son muy parecidas, despejando de los dos lados la velocidad radial, que ya sabemos que en un oscilador es la raíz cuadrada de la constante k entre la masa.

Por tanto nos queda, si aplicamos la generalidad de que empezamos en un ángulo de 90º(obviamente lo pasamos a radianes) la amplitud que hemos obtenido.

Hay que aclarar que esta es una ecuación de la trayectoria y es tan válida como cualquier otra, es decir, si nosotros empezamos desde otro ángulo, obtendremos otra constante, hemos hecho esto únicamente por facilitar el problema.

Por tanto a nosotros la ecuación de la trayectoria nos queda como:

Por tanto, el problema queda terminado.

Espero que os haya resultado interesante y hayáis aprendido bastante.

Si tenéis alguna duda, podéis dejármela en los comentarios.

Gracias.

TRABAJO Y ENERGÍA PARA MOVIMIENTOS RECTILÍNEOS

Hoy vamos a demostrar algunas fórmulas del trabajo y la energía que todos conocemos.

Supongamos una partícula que se mueve a lo largo del eje X bajo la acción de fuerzas independientes del tiempo, que solo actúan a lo largo de dicho eje, teniendo:

El trabajo como todos sabéis es fuerza por desplazamiento, escribimos la magnitud:

Bien, aquí lo que hemos hecho es sencillo.

En el paso 1 hemos establecido la magnitud del trabajo con un diferencial pues según el punto del eje dónde nos encontremos tenemos una fuerza por una diferencial de x referida al punto donde estamos.

En el paso 2 hemos integrado los dos lados de la igualdad pues teníamos dos diferenciales.

En el paso 3 por último hemos despejado quedándonos que el trabajo es la suma de cada diferencial de x entre dos puntos A y B por la fuerza que se le aplica, bueno, esto no es más que la definición de integral.

Una vez obtenido eso, sustituyamos esa fuerza por las distintas que conocemos, empecemos haciendo uso de la segunda ley de Newton:

Si sustituimos y operamos, vamos obteniendo resultados:

Bien, partiendo de la ecuación obtenida antes del trabajo.

En el paso 1 simplemente hemos sustituido la fuerza por la segunda ley de Newton, cabe destacar que la aceleración la hemos expresado como la derivada de la velocidad en función del tiempo, si por algún casual estás sufriendo para seguir estos planteamientos, pásate por mi blog de matemáticas o revisa otras entradas de este blog.

En el paso 2 hemos añadido dos diferenciales del tiempo, uno multiplicando y uno dividiendo para mantener la relación y que nos servirán más adelante en las operaciones, además hemos sacado la masa m pues es una constante fuera de la integral.

En el paso 3 hemos despejado el diferencial del tiempo que estaba multiplicando con el diferencial de tiempo  que dividía al diferencial de la velocidad y por otra parte hemos sustituido la derivada de x en función del tiempo por la velocidad.

En el paso 4 simplemente hemos obtenido esa ecuación operando las integrales, dejando la masa y poniendo el 1/2 como factor común.

En el paso 5 nos queda la ecuación que denominaremos energía cinética.

Bien, si F es continua e independiente del tiempo, podemos escribirla como:

Pues a la función V(x) la denominamos energía potencial.

Sustituyamos en la fórmula del trabajo:

En el paso 1 hemos sustituido la ecuación simplemente.

En el paso 2 y 3 hemos operado sustituyendo y haciendo las integrales.

Bien, como podemos observar el trabajo no es más que una variación de la energía potencial, de tal manera que el trabajo siempre es positivo si tendemos a disminuir la energía potencial.

Ahora que tenemos la definición de la energía cinética y potencial, vamos a igualarlas y a operar:

De lo que obtenemos que E=T+V, es decir, E, la denominada energía mecánica es la suma de las energías cinética y potencial.

Lo que significa el resultado anterior es que en 1D y para fuerzas que no dependen del tiempo, la energía mecánica es una constante del movimiento.

Bien, calculemos ahora la energía potencial para diversas fuerzas, empecemos con la ley de Hooke, que es una fuerza independiente del tiempo también.

Sustituyamos:

En el paso 1 hemos cogido la ecuación que liga el potencial y la fuerza, hemos despejado el potencial en el paso 2.

En el paso 3 hemos sustituido la fuerza por la ecuación de la ley de Hooke.

En el paso 4 hemos resuelto la ecuación y nos ha quedado el potencial relacionándolo con la ley de Hooke.

Veamos ahora que ocurre con la fuerza gravitatoria., también independiente del tiempo.

Sustituyamos ahora igual que antes:

El paso 1 es la ecuación normal de la fuerza gravitatoria.

En el paso 2 hemos sustituido esa fuerza en la ecuación del potencial, exactamente igual que en el ejemplo anterior.

En el paso 3 y ya con todo despejado obtenemos el potencial gravitatorio.

Espero que esta entrada demostrando algunas de las fórmulas más conocidad os haya resultado interesante.

Si tenéis alguna duda, podéis dejármela en los comentarios. 

Gracias.