Hoy vamos a demostrar algunas fórmulas del trabajo y la energía que todos conocemos.
Supongamos una partícula que se mueve a lo largo del eje X bajo la acción de fuerzas independientes del tiempo, que solo actúan a lo largo de dicho eje, teniendo:
El trabajo como todos sabéis es fuerza por desplazamiento, escribimos la magnitud:
Una vez obtenido eso, sustituyamos esa fuerza por las distintas que conocemos, empecemos haciendo uso de la segunda ley de Newton:
Ahora que tenemos la definición de la energía cinética y potencial, vamos a igualarlas y a operar:
Bien, calculemos ahora la energía potencial para diversas fuerzas, empecemos con la ley de Hooke, que es una fuerza independiente del tiempo también.
Supongamos una partícula que se mueve a lo largo del eje X bajo la acción de fuerzas independientes del tiempo, que solo actúan a lo largo de dicho eje, teniendo:
Bien, aquí lo que hemos hecho es sencillo.
En el paso 1 hemos establecido la magnitud del trabajo con un diferencial pues según el punto del eje dónde nos encontremos tenemos una fuerza por una diferencial de x referida al punto donde estamos.
En el paso 2 hemos integrado los dos lados de la igualdad pues teníamos dos diferenciales.
En el paso 3 por último hemos despejado quedándonos que el trabajo es la suma de cada diferencial de x entre dos puntos A y B por la fuerza que se le aplica, bueno, esto no es más que la definición de integral.Una vez obtenido eso, sustituyamos esa fuerza por las distintas que conocemos, empecemos haciendo uso de la segunda ley de Newton:
Si sustituimos y operamos, vamos obteniendo resultados:
Bien, partiendo de la ecuación obtenida antes del trabajo.
En el paso 1 simplemente hemos sustituido la fuerza por la segunda ley de Newton, cabe destacar que la aceleración la hemos expresado como la derivada de la velocidad en función del tiempo, si por algún casual estás sufriendo para seguir estos planteamientos, pásate por mi blog de matemáticas o revisa otras entradas de este blog.
En el paso 2 hemos añadido dos diferenciales del tiempo, uno multiplicando y uno dividiendo para mantener la relación y que nos servirán más adelante en las operaciones, además hemos sacado la masa m pues es una constante fuera de la integral.
En el paso 3 hemos despejado el diferencial del tiempo que estaba multiplicando con el diferencial de tiempo que dividía al diferencial de la velocidad y por otra parte hemos sustituido la derivada de x en función del tiempo por la velocidad.
En el paso 4 simplemente hemos obtenido esa ecuación operando las integrales, dejando la masa y poniendo el 1/2 como factor común.
En el paso 5 nos queda la ecuación que denominaremos energía cinética.
Bien, si F es continua e independiente del tiempo, podemos escribirla como:
Pues a la función V(x) la denominamos energía potencial.
Sustituyamos en la fórmula del trabajo:
En el paso 1 hemos sustituido la ecuación simplemente.
En el paso 2 y 3 hemos operado sustituyendo y haciendo las integrales.
Bien, como podemos observar el trabajo no es más que una variación de la energía potencial, de tal manera que el trabajo siempre es positivo si tendemos a disminuir la energía potencial.Ahora que tenemos la definición de la energía cinética y potencial, vamos a igualarlas y a operar:
De lo que obtenemos que E=T+V, es decir, E, la denominada energía mecánica es la suma de las energías cinética y potencial.
Lo que significa el resultado anterior es que en 1D y para fuerzas que no dependen del tiempo, la energía mecánica es una constante del movimiento.Bien, calculemos ahora la energía potencial para diversas fuerzas, empecemos con la ley de Hooke, que es una fuerza independiente del tiempo también.
Sustituyamos:
En el paso 1 hemos cogido la ecuación que liga el potencial y la fuerza, hemos despejado el potencial en el paso 2.
En el paso 3 hemos sustituido la fuerza por la ecuación de la ley de Hooke.
En el paso 4 hemos resuelto la ecuación y nos ha quedado el potencial relacionándolo con la ley de Hooke.
Veamos ahora que ocurre con la fuerza gravitatoria., también independiente del tiempo.
Sustituyamos ahora igual que antes:
El paso 1 es la ecuación normal de la fuerza gravitatoria.
En el paso 2 hemos sustituido esa fuerza en la ecuación del potencial, exactamente igual que en el ejemplo anterior.
En el paso 3 y ya con todo despejado obtenemos el potencial gravitatorio.
Espero que esta entrada demostrando algunas de las fórmulas más conocidad os haya resultado interesante.
Si tenéis alguna duda, podéis dejármela en los comentarios.
Gracias.






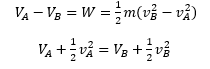




No hay comentarios:
Publicar un comentario