En esta entrada vamos a calcular el volumen de un elipsoide. Vamos a hacerlo con el método de integración en un conjunto numerable Jordan, que es aquel conjunto con volumen.
La teoría algebraica relacionada con este método de integración la pondré en otra entrada próximamente.
En este caso, el elipsoide es un conjunto tal que:
A es un rectángulo cerrado al cual pertenece el conjunto.
La teoría algebraica relacionada con este método de integración la pondré en otra entrada próximamente.
En este caso, el elipsoide es un conjunto tal que:
con a, b, c > 0.
La integral que tenemos que calcular es:
Pero para ello debemos comprobar en primer lugar que el volumen existe, esto es, que el conjunto sea medible Jordan.
Para ello vamos a decir que el conjunto es medible Jordan si la frontera del propio conjunto es de contenido cero.
Vamos a ver la frontera del conjunto entonces:
Tenemos que demostrar ahora que es de contenido cero.
Para ello tenemos que:
Es decir, lo que necesitamos es encontrar una función Ф que sea igual a la frontera de ese conjunto.
Para obtener esa función Ф veamos las coordenadas esféricas generalizadas para r=1.
Vemos que esa función, dependiente de los ángulos pertenece a la frontera del conjunto, pues sustituyendo da el valor 1.
Nos falta ver que k=[0, π]X[0, 2π] es compacto, es decir, es cerrado y acotado.
Vemos inmediatamente que es acotado, ahora comprobaremos si es cerrado.
donde k1 y k2, unidos por la intersección, tendrán que ser cerrados.
Bien, una vez hemos comprobado que es medible Jordan, vamos a pasar a resolver la integral, que será de la siguiente forma:
A es un rectángulo cerrado al cual pertenece el conjunto.
Bien, para resolver la siguiente integral realizaremos los siguientes pasos:
Primero fijaremos (x, y) e integraremos en z, por lo que el resultado dependerá de (x, y).
Después fijaremos x e integraremos en y, por lo que el resultado dependerá de x.
Finalmente integraremos en x.
En realidad estos pasos no son más que los pasos para resolver una simple integral triple que imagino que la mayoría de aquí sabréis resolver sin problemas.
Únicamente estoy añadiendo un poco de álgebra al cálculo integral, el futuras entradas abordaremos todas las incógnitas que nos haya dejado esta.
Fijemos (x, y):
Estos son los límites de integración para z.
(x, y) no pueden ser cualquiera ya que se encuentran dentro de una raíz y no puede acabar quedando negativa.
Fijamos ahora x:
Estos son los límites de integración para y.
x no puede ser cualquiera, debe tener un valor que acabe dando una raíz positiva.
Por ende los límites para x son:
Estos son los límites para x.
La integral al final queda:
Al hacer la primera integral respecto de z nos queda:
Vamos a hacer ahora la integral interior respecto de y:
Sacamos una raíz y para darnos cuenta que tenemos una raíz de 1 menos algo al cuadrado, por ende hagamos un cambio de variable.
Una vez hecho el cambio de variable y sabiendo que el ángulo varía entre 0 y π, desarrollemos la integral:
Un par de apuntes en el desarrollo de esta integral.
La raíz de uno menos coseno al cuadrado es igual a la raíz del seno al cuadrado, al estar entre 0 y π obtenemos el valor absoluto del seno.
Otro apunte es que el coseno de un ángulo entre 0 y 2π no contribuye, esto es, siempre va a dar el valor de cero.
Por último, realicemos la integral final:
El volumen de un elipsoide es, por tanto, 4/3πabc.
Se ve claramente que si fuese una esfera, los tres radios serían 1 y nos daría su volumen.
Si en cambio fuese un esferoide, dos de los radios serían 1.
Espero que esta entrada haya sido interesante y os ayude a entender y comprender la integración para volúmenes.
Si tenéis cualquier duda podéis dejármela en los comentarios.
Próximamente añadiré la teoría algebraica de las funciones integrales Riemann.
Además calcularé este volumen mediante el teorema de cambio de variables donde meteremos la definición de Jacobiano.
Gracias.

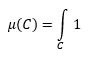
















No hay comentarios:
Publicar un comentario